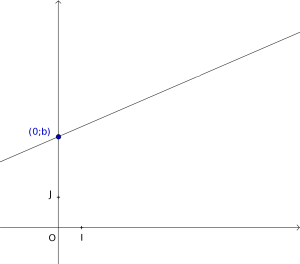
Coefficient directeur et ordonnée à l'origine
La droite représentative d'une fonction affine est définie par une équation réduite de la forme \(y=ax+b\)
Syntaxe : Vocabulaire
\(a\) est le coefficient directeur de la droite, il donne la pente.
\(b\) est l'ordonnée à l'origine de la droite, il donne la valeur de l'intersection avec l'axe des ordonnées.
Fondamental : Coefficient directeur
La pente de la droite est donnée par \(\color{red} a=\frac{\Delta y}{\Delta x}\) c'est à dire \(\frac{\text{variation en ordonnées}}{\text{variation en abscisses}}\)
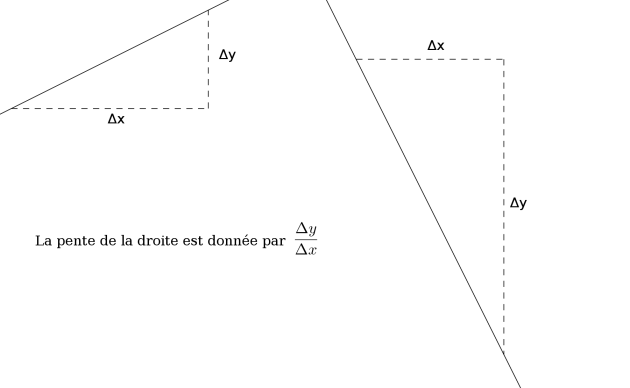
Le coefficient directeur indique le sens de variation de la fonction affine représentée :
Fondamental : Variations
Si \(a>0\) alors la fonction est croissante (la droite "monte").
Si \(a<0\) alors la fonction est décroissante (la droite "descend").
Si \(a=0\) alors la fonction est constante (la droite est parallèle à l'axe des abscisses ou "horizontale").
Fondamental : Ordonnée à l'origine
L'ordonnée à l'origine est l'ordonnée du point de la droite d’abscisse 0 : \((0\ ;\ \textcolor{blue}{b})\)
L'appellation ordonnée à l'origine n'est pas réservée aux droites (représentatives de fonctions affines), elle est valable pour toutes les courbes représentatives de fonctions.
Fondamental :
On pourra dire, en général, que : si la courbe est la représentation graphique d'une fonction \(f\) alors l'ordonnée à l'origine est \(\textcolor{blue}{f(0)}\).