Calcul des racines
Définitions
Les racines du trinôme \(ax^2+bx+c\) sont les solutions, si elles existent, de l'équation \(ax^2+bx+c=0\)
Méthode : Résolution graphique
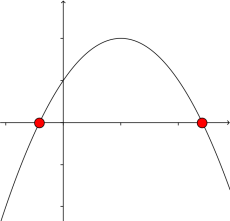
Les racines du trinôme \(ax^2 +bx +c\) sont les abscisses des points d'intersection, s'ils existent, entre la courbe représentative du trinôme et l'axe des abscisses.
(exemple ci-contre pour deux racines)
Méthode : Utilisation de la calculatrice
Complément : Calcul algébrique des racines
Si on ne dispose pas de calculatrice permettant d'obtenir directement les racines, on peut effectuer le calcul algébrique.
On calcule d'abord le discriminant noté \(\Delta\) : \(\Delta=b^2-4ac\)
En fonction du signe de \(\Delta\), on calcule la valeur des racines, si elles existent.
si \(\Delta>0\) il y a 2 racines : \(x_1=\frac{-b-\sqrt{\Delta}}{2a}\) et \(x_2=\frac{-b+\sqrt{\Delta}}{2a}\)
si \(\Delta=0\) il y a une seule racine (racine double) : \(x_0=\frac{-b}{2a}\)
si \(\Delta<0\) il n'y a pas de racine réelle.