Résolution graphique d'inéquations

Comparer f et g

Soit deux fonctions \(f\) et \(g\) définies sur leurs ensembles de définition respectifs \(D_f\) et \(D_g\) et leurs courbes représentatives \(\mathcal{C}_f\) et \(\mathcal{C}_g\).

Fondamental :

Les solutions de l'inéquation \(f (x)\geqslant g (x)\) (respectivement \(f (x) > g (x)\) ) sont les abscisses des points pour lesquels la représentation graphique de \(f\) est au-dessus (respectivement strictement au-dessus) de la représentation graphique de \(g\).

Les solutions de l'inéquation \(f (x)\leqslant g (x)\) (respectivement \(f (x) < g (x)\) ) sont les abscisses des points pour lesquels la représentation graphique de \(f\) est au-dessous (respectivement strictement au-dessous) de la représentation graphique de \(g\).

Exemple :

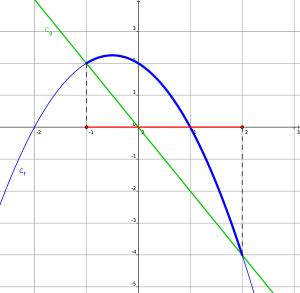
Les solutions de l'inéquation \(f(x)\geqslant g(x)\) sont les abscisses des points pour lesquels \(C_f\) est au dessus de \(C_g\).

Ici la courbe \(\color{blue}C_f\) est au-dessus de \(\color{green}C_g\) pour les valeurs de \(x\) comprises entre -1 et 2.

Pour \(x=-1\) et \(x=2\) on a \(f'x)=g(x)\)donc

l'ensemble des solutions de \(f(x)\geqslant g(x)\) est \(S=[-1 ;2]\).

l'ensemble des solutions de \(f(x)> g(x)\) est \(S=]-1 ;2[\).

Comparer f à une constante

Soit la fonction \(f\) définie sur son ensemble de définition \(D_f\) et sa courbe représentative \(\mathcal{C}_f\).

Remarque :

L’inéquation \(f(x)\geqslant k\) est un cas particulier de \(f(x)\geqslant g(x)\) avec \(g(x)=k\).

(idem pour \(f(x)> k\), \(f(x)\leqslant k\) et \(f(x)< k\))

Fondamental :

Les solutions de l'inéquation \(f(x)\geqslant k\) (respectivement \(f (x) > k\) ) sont les abscisses des points de la représentation graphique de \(f\) dont l'ordonnée est supérieure ou égale (respectivement strictement supérieure) à \(k\).

Les solutions de l'inéquation \(f(x)\leqslant k\) (respectivement \(f (x) < k\) ) sont les abscisses des points de la représentation graphique de \(f\) dont l'ordonnée est inférieure ou égale (respectivement strictement inférieure) à \(k\).

Exemple :

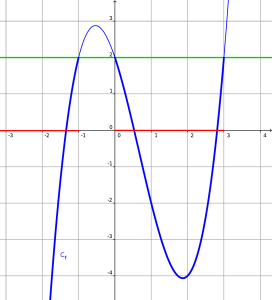
Les solutions de l'inéquation \(f(x)\leqslant 2\) sont les abscisses des points de \(C_f\) d'ordonnée inférieure ou égale à 2.

Ici les points de \(C_f\) d'abscisses comprises entre \(-\infty\) et -1 ou entre 0 et 3 ont une ordonnée inférieure ou égale à 2 donc l'ensemble des solutions de \(f(x)\leqslant 2\) est \(S=]-\infty ;-1]\cup[0 ;3]\).

Signe de f

Soit la fonction \(f\) définie sur son ensemble de définition \(D_f\) et sa courbe représentative \(\mathcal{C}_f\).

Remarque :

L’inéquation \(f(x)\geqslant 0\) est un cas particulier de \(f(x)\geqslant k\) avec \(k=0\).

(idem pour \(f(x)> 0\), \(f(x)\leqslant 0\) et \(f(x)<0\))

Fondamental :

Les solutions de l'inéquation \(f(x)\geqslant 0\) (respectivement \(f (x) > 0\) ) sont les abscisses des points pour lesquels la représentation graphique de \(f\) est au-dessus (respectivement strictement au-dessus) de l'axe des abscisses.

Les solutions de l'inéquation \(f(x)\leqslant 0\) (respectivement \(f(x)< 0\) ) sont les abscisses des points pour lesquels la représentation graphique de \(f\) est au-dessous (respectivement strictement au-dessous) de l'axe des abscisses.

Exemple :

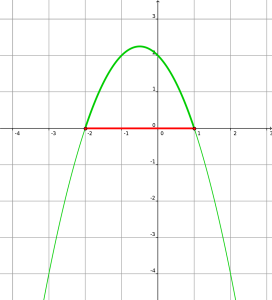
Les solutions de l'inéquation \(f(x)> 0\) sont les abscisses des points pour lesquels la représentation graphique de \(f\) est strictement au-dessus de l'axe des abscisses.

Ici la courbe \(C_f\) est au-dessus de l'axe des abscisses pour \(x\) compris entre -2 et 1 donc l'ensemble des solutions de \(f(x)>0\) est \(S=]-2 ;1[\).

On en déduit que \(f(x)\leqslant 0 \)pour les autres valeurs de x c'est-à-dire l'ensemble \(]-\infty ;-2]\cup [1 ;+\infty[\).

Remarque :

Résoudre les inéquations \(f(x)\geqslant 0\) ou \(f(x)\leqslant 0\) permet d'étudier le signe de la fonction \(f\).