Déterminer graphiquement une équation réduite de droite
Fondamental :
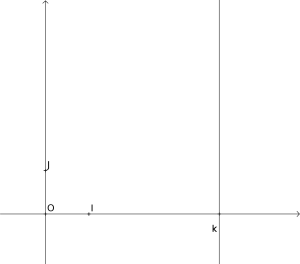
L'équation d'une droite verticale s'écrit \(x=k\).
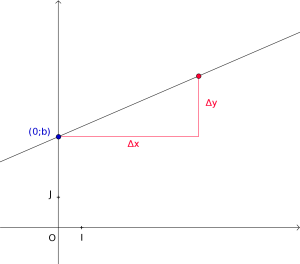
L'équation réduite d'une droite représentant une fonction affine s'écrit \(y=ax+b\).
Méthode : Droite représentant une fonction affine
On cherche la valeur de \(a\) et la valeur de \(b\)
On lit l'ordonnée à l'origine de la droite : \(\color{blue}b\)
On choisit deux points aux coordonnées précises et on lit la pente (coefficient directeur) entre ces deux points : \(\color{red}a=\frac {\Delta y}{\Delta x}\)
\(y=\textcolor{red}{a}x+\textcolor{blue}{b}\)
Remarque : Cas particuliers parmi les fonctions affines
Si la droite est horizontale, le coefficient directeur est égal à 0. L'équation sera de la forme \(y=b\) et représente une fonction constante.
-----
Si la droite passe par l'origine, l'ordonnée à l'origine est égale à 0. L'équation sera de la forme \(y=ax\) et représente une fonction affine.
Méthode : Droite verticale
On cherche la valeur de \(k\).
On lit l'abscisse des points de la droite : \(k\)
\(x=k\)
Remarque :
Une droite verticale ne représente pas une fonction.