Fonction affine
Une fonction affine est représentée par une droite donc son signe est lié à ses variations.
Le changement de signe se fait pour la racine de la fonction.
Méthode :
On observe les variations de \(x \mapsto ax+b\) et on calcule la racine de la fonction.
Méthode : Constante
La fonction \(x \mapsto b\) est constante donc elle est du signe de \(b\).
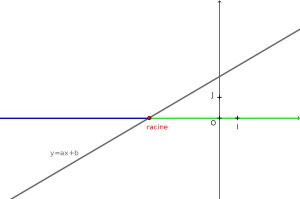
Méthode : Croissante
Si \(a>0\) alors la fonction \(x \mapsto ax+b\) est croissante donc elle est négative, elle s’annule puis elle est positive.
On peut dresser le tableau de signe de \(ax+b\).
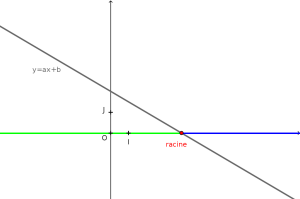
Méthode : Décroissante
Si \(a<0\) alors la fonction \(x \mapsto ax+b\) est croissante donc elle est positive, elle s’annule puis elle est négative.
On peut dresser le tableau de signe de \(ax+b\) :