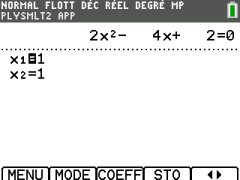
Calcul des racines du trinôme à la calculatrice TI
La calculatrice résout les équations de la forme \(ax^2+bx+c=0\).
Il faut donc identifier \(a\), \(b\) et \(c\).
Syntaxe :
puis pour \(\small{\textcolor{white}{\colorbox{black}{SOLVEUR}}}\) choisir \(\small{\textcolor{white}{\colorbox{black}{2:}}}\textsf{ Plysmlt2}\).
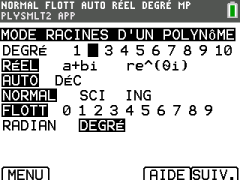
Choisir ensuite \(\small{\textcolor{white}{\colorbox{black}{1:}}}\textsf{ RACINES D'UN POLYNÔME}\) puis vérifier que les réglages sont ceux de la fenêtre suivante et appuyer sur 
[SUIV.]
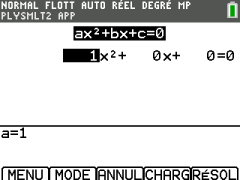
La fenêtre suivante s'ouvre.
Vous devez y renseigner les valeurs de \(a\), \(b\) et \(c\).
Exemple : Exemple
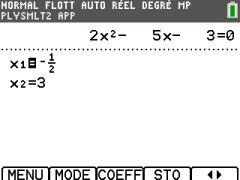
Résoudre \(2x^2-5x-3=0\)
On a \(a=2\), \(b=-5\) et \(c=-3\)
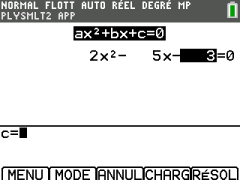
On appuie sur ou sur [RÉSOL] pour lancer la résolution de l'équation.
On obtient 2 solutions : \(-\frac{1}{2}\) et 3
Complément : Complément
S'il n'y a pas de racines (pas de solutions), la calculatrice l'indique.
S'il y a une seule racine, elle est notée deux fois parce que la racine unique est aussi appelée « racine double ».
