Exercice : MD3 - page 47
Question
Question
Déterminer le signe de \(2 x – 3\) suivant les valeurs de \(x\) .
Solution
\(\begin{array}{|c|lcccr|}\hline x & -\infty &&\frac{3}{2}&&+\infty \\\hline \text{signe de } 2x+3 &&-&0&+&\\\hline\end{array}\)
Solution
La fonction affine \(x \mapsto 2x-3\) est croissante car \(a>0\) et elle s'annule en \(\displaystyle x=\frac{3}{2}\).
Question
La population d'une ville est de 30 000 habitants en 2020 et on considère qu'elle va croître pour les années à venir de 2 % par an.
À combien d'habitants s'élèvera sa population en 2025 ? Arrondir à l'unité.
Indice
On peut se reporter au cours de 2nde concernant les évolutions en pourcentage.
Indice
évolution répétée 5 fois donc 5 évolutions successives
Solution
33 122 habitants à l'unité près.
Solution
le coefficient multiplicateur associé à une augmentation de 2% est 1,02. On effectue cette évolution successivement 5 fois donc un coefficient global de \(1,02^5\) d'où : \(30\ 000 \times 1,02^5 \approx 33\ 122\)
Question
On sait qu'un ordre de grandeur de \(2^{10}\) est \(1\ 000\). Donner un ordre de grandeur de \(2^{30}\) .
Indice
Rappel puissances
Solution
1 000 000 000
Solution
\(2^{30}=\left(2^{10}\right)^3\approx 1000^3\)
Question
Résoudre l'équation \(2 x^ 2 = 98\).
Indice
Deux méthodes :
Annuler le deuxième membre de l'égalité, factoriser l'identité remarquable et résoudre (produit nul)
Isoler \(x^2\) puis prendre la racine carrée et son opposé
Solution
\(S=\{-7 ; 7\}\)
Solution
1ère méthode
\(2x^2=98\)
\(x^2=49\)
\(x^2-49=0\)
on remarque que \(x^2-49\) est l'identité remarquable \(a^2-b^2=(a-b)(a+b)\)
\((x-7)(x+7)=0\)
Un produit de facteur est nul si et seulement si un des facteurs est nul donc \(x=7\) ou \(x=-7\)
2ème méthode
\(2x^2=98\)
\(x^2=49\) et on sait que \(7^2=49\)
\(x=-\sqrt{49}=-7\) ou \(x=\sqrt{49}=7\)
Question
Question
Le prix d'un produit augmente dans un premier temps de 20 %, puis diminue de 20 %.
Indiquer comment a évolué le prix et de quel pourcentage.
Indice
On peut se reporter au cours de 2nde concernant les évolutions en pourcentage
ou utiliser que 10% c'est un dixième.
Solution
Baisse de 4%
Solution
avec les coefficients multiplicateurs
Hausse de 20% : c=1,20
baisse de 20% : c=0,80
\(1,2 \times 0,8\)
on fait \(8 \times 12 = 8 \times 10 + 8 \times 2 = 80 + 16 = 96\) qu'on divise par 100 donc un coef de 0,96 d’où une baisse de 4%
avec les dixièmes
20% c'est deux dixièmes :
pour 100, une hausse de 20% est une augmentation de 20 donc donne 120.
pour 120 une baisse de 20% est une baisse de \(2\times 12=24\).
On a augmenté de 20 et baissé de 24 donc au final c'est une baisse de 4 pour 100 au départ.
Question
Question
Le graphique ci-dessous représente le nombre de naissances en France depuis 2011.
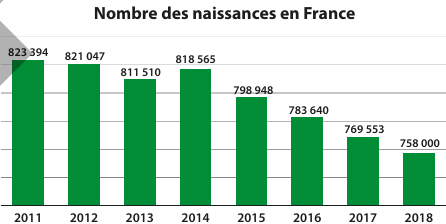
1) Déterminer le nombre moyen de naissances sur les huit dernières années.
2) Déterminer le taux d'évolution des naissances entre 2011 et 2018.
Indice
On peut se reporter au cours de 2nde concernant les évolutions en pourcentage.
Solution
1) 798 082,125
2) baisse d'environ 8%
Solution
1) \(\displaystyle \frac{823 394 + \cdots \cdots + 758 000}{8}=798\ 082,125\)
2) on cherche le pourcentage d'évolution entre 823 394 et 758 000.
1ère méthode : \(\displaystyle \frac{758 000 }{823 394 } \approx 0,92\) donc la valeur finale est 92% de la valeur initiale : une baisse de 8%
2ème méthode : \(\displaystyle \frac{758 000-823 394 }{823 394 } \approx -0,08\) soit une baisse de 8%