Exercice : MD7 - page 85
Question
On considère les fonctions \(f\) et \(h\) représentées ci-contre.
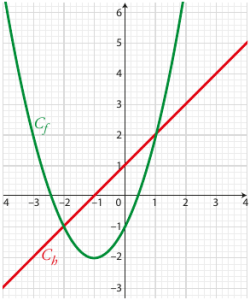
Déterminer l'image de – 3 par \(f\).
Indice
Lecture graphique d'image
Solution
L'image de -3 par la fonction \(f\) est 2.
Question
On considère les fonctions \(f\) et \(h\) représentées ci-contre.
Construire le tableau de variations de \(f\).
Solution
\(\begin{array}{|c|lcccr|}\hline x&-4&&-1&&4\\\hline variations&f(-4)&&&&f(4)\\de&&\searrow&&\nearrow&\\f&&&-2&&\\\hline\end{array}\)
Question
On considère les fonctions \(f\) et \(h\) représentées ci-contre.
Résoudre \(f(x)<h(x)\)
Indice
Résoudre graphiquement une inéquation
et attention aux bornes.
Solution
Les solutions de l'inéquation \(f(x)<h(x)\) sont les abscisses des points de la courbe de \(f\) qui sont en dessous de la courbe de \(h\) : \(\mathrm{S}=]-2 ;1[\)
Question
Question
Question
Question
Résoudre \(4x^2-3=21\).
Indice
Deux méthodes :
Annuler le deuxième membre de l'égalité, factoriser l'identité remarquable et résoudre (produit nul)
Isoler \(x^2\) puis prendre la racine carrée et son opposé
Solution
\(\mathrm{S}=\left\{-\sqrt{6} ;\sqrt{6}\right\}\)
Solution
1ère méthode
\(4x^2-3=21\)
\(4x^2-24=0\)
\(4(x^2-6)=0\)
on remarque que \(x^2-6\) est l'identité remarquable \(a^2-b^2=(a-b)(a+b)\)
\((x-\sqrt{6})(x+\sqrt{6})=0\)
Un produit de facteur est nul si et seulement si un des facteurs est nul donc \(x=\sqrt{6}\) ou \(x=-\sqrt{6}\)
2ème méthode
\(4x^2-3=21\) équivaut à \(4x^2=24\)
équivaut à \(x^2=6\)
donc \(x=-\sqrt{6}\) ou \(x=\sqrt{6}\)
Question
En 2019, l’huître creuse spéciale de claire de calibre M3 s'est vendue 85 € la bourriche de 100 pièces au marché de Rungis et 110 € la bourriche de 200 pièces.
Donner le pourcentage de réduction si l'on achète une bourriche de 200 pièces par rapport à deux bourriches de 100 pièces.
Indice
Évolution par
Solution
réduction de 35,3%
Solution
2 bourriches de 100 pièces : \(85\times2=170\)
au lieu de 110 pour la bourriche de 200 pièces.
Coefficient multiplicateur
le coefficient multiplicateur est : \(\displaystyle \frac{110}{170}\approx 0,647\) donc une réduction de 35,3% \((64,7-100)\)
Évolution absolue
L'évolution absolue est -60€ \((110-170)\) donc \(\displaystyle \frac{-60}{170}\approx -0,353\) donc une réduction de 35,3%
Question
D'après le graphique ci-contre, indiquer si l'ensemble des compagnies japonaises réunies auraient été numéro un mondial du transport de passagers en 2016. Justifier.
Solution
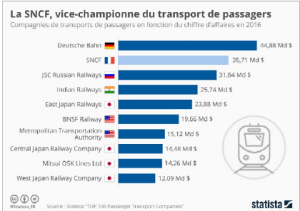
\(23,88+14,48+14,26+12,09\) fait plus de 60 Md $ donc oui l'ensemble des compagnie japonaise réunies auraient été numéro un mondial du transport de passagers en 2016.