MA1 - page 257 [Automatismes]

Exercice : MA1 - page 257

Question

Calculer \(\displaystyle 1-\frac{2}{3}\times\frac{3}{5}\).

Solution

\(\displaystyle 1-\frac{2}{3}\times\frac{3}{5}=1-\frac{2}{5}=\frac{3}{5}\)

Question

Le relevé de températures moyennes quotidiennes en degrés Celsius (°C) à Aurillac durant une semaine de novembre donne les valeurs suivantes : 9,5 ; 6,5 ; 3,5 ; 6,2 ; 7,3 ; 4,1 ; 6,9.

Déterminer la température moyenne sur Aurillac cette semaine-là.

Question

Le relevé de températures moyennes quotidiennes en degrés Celsius (°C) à Aurillac durant une semaine de novembre donne les valeurs suivantes : 9,5 ; 6,5 ; 3,5 ; 6,2 ; 7,3 ; 4,1 ; 6,9.

Déterminer la température médiane sur Aurillac cette semaine-là.

Solution

On classe par ordre croissant : 3,5 ; 4,1 ; 6,2 ; 6,5 ; 6,9 ; 7,3 ; 9,5.

Il y a 7 valeurs donc la médiane est la 4ème (3 inférieures et 3 supérieures) donc Me=6,5

Question

Factoriser \((2 x − 3)( x + 2) + (1 − 2 x )(2 x − 3)\).

Solution

\((2 x − 3)( x + 2) + (1 − 2 x )(2 x − 3)\)

\((2x-3)\left[(x+2)+(1-2x)\right]\)

\((2x-3)(x+2+1-2x)\)

\((2x-3)(3-x)\)

Question

Écrire \(4^5\times4^7\) sous forme d'une puissance de 2.

Solution

\(4^5\times4^7=4^{5+7}=4^{12}\)

\(\displaystyle 4^{12}=\left(2^2\right)^{12}=2^{2\times12}=2^{24}\)

Question

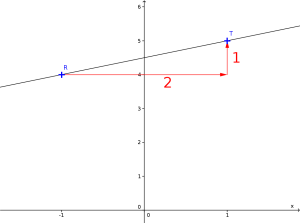
Déterminer l'équation réduite de la droite (RT) avec R(−1 ; 4) et T(1 ; 5).

Solution

\(\displaystyle y=\frac{1}{2}x+\frac{9}{2}\)

\(y=0,5x+4,5\)

Solution

Méthode graphique :

Par lecture graphique : \(a=\displaystyle\frac{1}{2}=0,5\) et \(b=4,5\)

Méthode algébrique :

\(y=ax+b\) avec \(\displaystyle a=\frac{5-4}{1-(-1)}=\frac{1}{2}\)

\(\displaystyle y=\frac{1}{2}x+b\) et (1 ; 5) appartient à la droite

\(\displaystyle 5=\frac{1}{2}\times1+b\) donc \(\displaystyle b=5-\frac{1}{2}\)

\(\displaystyle y=\frac{1}{2}x+\frac{9}{2}\)

Question

Résoudre l'équation \(2 x − 1 = 15 − 3 x\) .

Solution

\(2 x − 1 = 15 − 3 x\)

\(2x+3x=15+1\)

\(5x=16\)

\(\displaystyle x=\frac{16}{5}\)

Question

En horticulture, pour une surface de 1 m² , si on note N le nombre de végétaux que l'on peut planter et D la distance en mètres attendue entre chaque végétal, la relation \(\mathrm{N\times D^2 = 1}\) doit être vérifiée.

Déterminer la distance attendue entre chaque végétal, arrondie au cm, si on veut planter cinq végétaux sur une surface de 1 m² .

Indice

Remplacer N pour obtenir l'équation et résoudre.

Indice

L'équation est \(5\times\rm{D}^2=1\)

Solution

\(\displaystyle \rm{D}=\frac{1}{\sqrt{5}}\approx0,447\)

Solution

On résout : \(5\times\rm{D}^2=1\)

\(\displaystyle \rm{D}^2=\frac{1}{5}\)

puisque D est une distance, seule la solution positive nous intéresse : \(\displaystyle \rm{D}=\sqrt{\frac{1}{5}}=\frac{1}{\sqrt{5}}\)

Question

Donner l'ordonnée du point d'abscisse 4 appartenant à la courbe représentative de la fonction \(f\) définie pour tout réel \(x \ne 1\) par \(\displaystyle f(x)=\frac{3x-1}{1-x}\)

\(\displaystyle f(4)=\frac{11}{-3}\)

Question

Suite à un engouement sur une marque de baskets, une paire dont le prix est de 95 € augmente de 10 %. Calculer son prix après augmentation.