Exercice : MC7 - page 149
Question
Développer \((1 + h )^3\) en l'écrivant \((1 + h )^2 × (1 + h )\).
Indice
\((1+h)^3=(1+h)^2\times (1+h)\)
Développer l'identité remarquable \((1+h)^2\) puis multiplier le résultat par \((1+h)\).
Solution
\((1+h)^3=1+3h+3h^2+h^3\)
Solution
\((1+h)^3\)
\((1+h)^2\times (1+h)\)
\((1+2h+h^2)(1+h)\)
\(1+2h+h^2+h+2h^2+h^3\)
\(1+3h+3h^2+h^3\)
Question
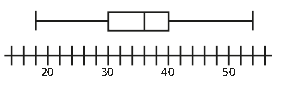
On donne le diagramme en boite ci-dessous, résultat d'un sondage sur un échantillon de 1 000 personnes auxquelles on a demandé leur âge.
Calculer l'étendue et indiquer la médiane de cet échantillon.
Indice
La boite indique les trois quartiles et les moustaches donnent les valeurs extrêmes.
Solution
étendue :
\(valeur_{max}-valeur_{min}\)
\(54-18=36\)
médiane :
36
Question
On donne le diagramme en boite ci-dessous, résultat d'un sondage sur un échantillon de 1 000 personnes auxquelles on a demandé leur âge.
Donner le pourcentage de personnes de cet échantillon dont l'âge est inférieur à 40 ans.
Solution
40 correspond à la valeur supérieure de la boite donc au 3ème quartile : au moins 75% des personnes sont âgées de moins de 40 ans.
Question
Question
Réduire au même dénominateur l'expression suivante, la développer et réduire le numérateur et le dénominateur :
\(\displaystyle\frac{1-5y}{4}+\frac{7}{2y-1}\)
Solution
\(\displaystyle\frac{1-5y}{4}+\frac{7}{2y-1}=\frac{-10y^2+7y+27}{8y-4}\)
Solution
\(\displaystyle\frac{1-5y}{4}+\frac{7}{2y-1}\)
\(\displaystyle\frac{(2y-1)(1-5y)}{(2y-1)\times 4}+\frac{4\times7}{4\times (2y-1)}\)
\(\displaystyle\frac{2y-10y^2-1+5y}{8y-4}+\frac{28}{8y-4}\)
\(\displaystyle\frac{-10y^2+7y+27}{8y-4}\)
Question
Donner le coefficient multiplicateur correspondant à une baisse de 8%.
Indice
Évolution en pourcentage.
Solution
0,92
Solution
\(100-8=92\) donc il reste 92% de la valeur initiale : le coefficient multiplicateur vaut 0,92.
Question
Étudier le signe de \((−3 x + 4)(2 x + 8)\).
Indice
signe de chaque facteur et règle du signe d'un produit (résumé dans un tableau)
ou
remarquer que c'est un polynôme du second degré dont les racines sont faciles à trouver (sous la forme factorisée)
Solution
\(\begin{array}{|c|lcccccr|}\hline x&-\infty&&-4&&\frac{4}{3}&&+\infty\\\hline\text{signe de }(−3 x + 4)(2 x + 8)&&-&0&+&0&-&\\\hline\end{array}\)
Solution
Les racines sont \(\frac{4}{3}\) pour \((-3x+4)\) et -4 pour \((2x+8)\)
signe de chaque facteur et règle du signe d'un produit
On fait un tableau de signe :
\(\begin{array}{|c|lcccccr|}\hline x&-\infty&&-4&&\frac{4}{3}&&+\infty\\\hline\text{signe de }(-3x+4)&&+&&+&0&-&\\\hline\text{signe de }(2x+8)&&-&0&+&&+&\\\hline\hline\text{signe de }(−3 x + 4)(2 x + 8)&&-&0&+&0&-&\\\hline\end{array}\)
signe du trinôme
Si on commence à développer on obtient : \((−3 x + 4)(2 x + 8)=-6x^2 \cdots\cdots\).
donc c'est un trinôme qui a deux racines avec \(a=-6\) donc \(a<0\) donc la concavité de la parabole est tournée vers le bas et le signe sera donc \(- ; + ; -\) donc
\(\begin{array}{|c|lcccccr|}\hline x&-\infty&&-4&&\frac{4}{3}&&+\infty\\\hline\text{signe de }(−3 x + 4)(2 x + 8)&&-&0&+&0&-&\\\hline\end{array}\)
Question
Dans le cas du remboursement d'un prêt de capital \(C\) en euros, sur \(n\) mois au taux annuel \(t\) %, la mensualité \(m\) se calcule par la formule suivante : \(\displaystyle m=\frac{C\times\frac{t}{1200}}{1-\left(1+\frac{t}{1200}\right)^{-n}}\)
Calculer la mensualité correspondant au remboursement du prêt d'un capital de 170 000 € sur 17 ans au taux annuel de 2,5 %.
Indice
\(n\) est en mois
Solution
\(m=1023,78\)
Solution
\(\displaystyle m=\frac{170 000\times\frac{2,5}{1200}}{1-\left(1+\frac{2,5}{1200}\right)^{-17\times 12}}\)
