MD5 - page 67 [Automatismes]

Exercice : MD5 - page 67

Question

« Selon les estimations au 1^er novembre 2019, la production viticole 2019 s'établirait à 42,2 millions d' hectolitres. La récolte viticole 2019 serait inférieure de 15 % à celle de 2018. »

(Source : http://agreste.agriculture.gouv.fr/IMG/pdf/IRVin_Novembre2019.pdf)

1) Donner le nombre de bouteilles de vin de 75 cL que l'on peut obtenir avec 42,2 millions hL produit.

2) Estimer la récolte viticole de 2018.

Indice

1hL=100L et 1L=100cL

On peut se reporter au cours de 2^nde concernant les évolutions en pourcentage.

Solution

1) 5626 666 666 bouteilles de 75 cL

2) En 2018 il y a eu 49,45 millions d'hL de vin

Solution

1) 42,2 million d'hL= \(42,2 \times 100 \times 100\) millions donc \(422\ 000\div 75\) millions de bouteilles soit 5626 666 666 bouteilles entières.

2) la baisse de 15% est associée au coefficient multiplicateur 0,85 pour passer de 2018 à 2019 donc \(0,85\times \text{prod de 2018 } = 42,2 \text{millions}\)

donc la production de 2018 est \(42,2\div 0,85= 49,45\)

Question

Développer \(2 x (1 – 3 x ) – ( x + 1)(4 x + 2)\).

Indice

Développements

Solution

\(-10x^2-4x-2\)

Solution

\(2 x (1 – 3 x ) – ( x + 1)(4 x + 2)\)

\(2x-6x^2-(4x^2+2x+4x+2)\)

\(2x-6x^2-4x^2-2x-4x-2\)

\(-10x^2-4x-2\)

Question

Convertir 54 kilomètres par heure en mètres par seconde.

Indice

1km = 1000 m

dans 1 heure il y a 3600 secondes

Solution

15 m par seconde

Solution

54km = 54000 m

54000 m par heure donc 54 000 m par 3600 secondes donc \(54\ 000 \div 3\ 600=540 \div 36\)

On simplifie : \(\displaystyle \frac{6\times 9 \times 10}{4\times9}=\frac{6 \times 10}{4}=\frac{2\times3\times 10}{2\times 2}=\frac{3\times 10}{2}=1,5\times 10=15\)

Question

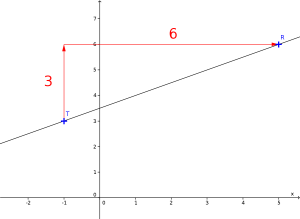
Déterminer l'équation réduite de la droite (RT) où R(5 ; 6) et T(– 1 ; 3).

Graphiquement

\(\displaystyle a=\frac{3}{6}=0,5\)

\(b=3,5\)

Algébriquement

\(\displaystyle a=\frac{6-3}{5-(-1)}=\frac{3}{6}=\frac{1}{2}\)

Le point R(5 ; 6) appartient à la droite \(\displaystyle y=\frac{1}{2}x+b\)

donc \(\displaystyle 6=\frac{1}{2}\times 5+b\)

\(\displaystyle 6-\frac{5}{2}=b\)

\(\displaystyle \frac{7}{2}=b\)

donc \(\displaystyle (\mathsf{RT}) :y=\frac{1}{2}x+\frac{7}{2}\)

Question

On considère la fonction \(f\) définie pour tous les réels par \(f ( x ) = x^3 – 3 x^ 2 + 2\).

1) Déterminer \(f ' ( x )\).

2) Donner l'image de – 1 par \(f\) .

3) Résoudre \(f ( x ) = 2\).

Indice

1) dérivée d'un polynôme

2) on remplace

3) factorisation puis produit nul.

Solution

1) \(f'(x)=3x^2-6x\)

2) \(f ( -1) = 0\)

3) \(S=\{0 ; 3\}\)

Solution

1) \(f'(x)=3x^2-6x\)

2) \(f ( -1) = (-1)^3 – 3 \times (-1)^ 2 + 2\)

\(f(-1)=-1-3\times 1 +2 = 0\)

3) \(x^3 – 3 x^ 2 + 2=2\)

\(x^3-3x^2=0\)

\(x^2(x-3)=0\)

donc \(x^2=0\) ou \(x-3=0\)

\(S=\{0 ; 3\}\)

Question

Déterminer le taux équivalent à deux augmentations, l'une de 25% puis l'autre de 12%.

\(1,25 \times 1,12 = 1,4\)

Un coefficient multiplicateur de 1,4 traduit une augmentation de 40%

Question

Le nombre de livres vendus chaque année en millions d'unités est donné par le tableau suivant :

2010	2011	2012	2013	2014	2015	2016	2017
451,9	450,6	440,9	426,8	421,8	436,7	434,5	430

(Source : SNE/Société des gens de lettres, https://www.sgdl.org/sgdl-accueil/le-guide-pratique/le-secteur-du-livre)

Déterminer le nombre moyen de livres vendus par an sur cette période.

Solution

436,65

Solution

\(\displaystyle \frac{451,9 + \cdots \cdots +430}{8}\)