Exercice : MC3 - page 115
Question
Calculer \(\displaystyle \left(\frac{1}{3}\right)^2-2\times \frac{1}{3}\)
Indice
Calculer le carré puis réduire au même dénominateur.
Solution
\(\displaystyle -\frac{5}{9}\)
Solution
\(\displaystyle \left(\frac{1}{3}\right)^2-2\times \frac{1}{3}\)
\(\displaystyle \frac{1}{9}- \frac{2}{3}\)
\(\displaystyle \frac{1}{9}-\frac{2\times 3}{3\times3}\)
\(\displaystyle \frac{1}{9}-\frac{6}{9} = -\frac{5}{9}\)
Question
Dans la région Grand Est, le nombre d'exportations de gros bovins est passé de 15 333 en 2018 à 17 126 en 2019. Déterminer l'évolution en pourcentage.
Solution
Une augmentation d'environ 11,7%
Solution
\(\displaystyle\frac{17126}{15333}\approx1,1169\) c'est le coefficient multiplicateur
\(1-1,1169=0,1169\) soit environ 11,7%
ou
\(\displaystyle\frac{17126-15333}{15333}\approx0,1169\) soit environ 11,7%
Question
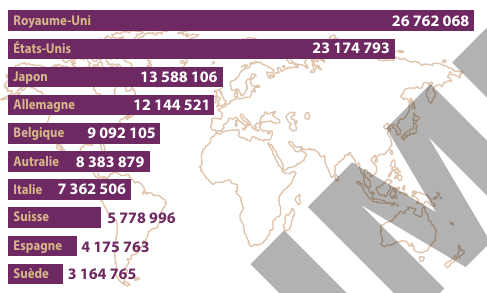
Le graphique ci-dessous montre les dix plus gros importateurs de champagne ainsi que le nombre de bouteilles vendues dans le pays. Déterminer le pourcentage de vente de bouteilles que représentent à eux les États-Unis et le Royaume-Uni par rapport à l'ensemble de ces dix pays.
(« source deux : https://www.champagne.fr/fr/economie/chiffres-clef »
)
Indice
« par rapport »
se traduit par une fraction.
Solution
Les États-Unis et le Royaume-Uni représente environ 44% de l'ensemble de ces dix pays
Solution
On calcule la vente des États-Unis et du Royaume-Uni : \(26\ 762\ 068+23\ 174\ 793=49\ 936\ 861\)
Pour l'ensemble de ces dix pays, la somme donne : \(113\ 627\ 502\)
Le rapport : \(\displaystyle\frac{49\ 936\ 861}{113\ 627\ 502}\approx 0,439\) soit environ 44%
Question
On considère la fonction \(f\) définie sur l'intervalle [–3 ; 5] représentée par la parabole \(C_f\).
Résoudre \(f (x) \geqslant 0\).
Indice
Lecture graphique d'inéquations.
Solution
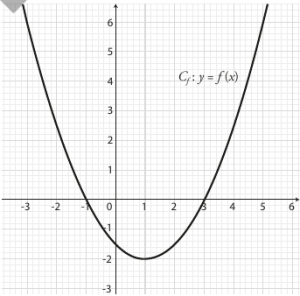
Les solutions de \(f(x)\geqslant 0\) sont les valeurs de \(x\) pour lesquelles la courbe \(C_f\) est au dessus de l'axe des abscisses : \(S=[-3 ; -1]\cup [3 ;5]\)
Question
On considère la fonction \(f\) définie sur l'intervalle [–3 ; 5] représentée par la parabole \(C_f\).
Déterminer graphiquement \(f (4)\).
Déterminer le(s) antécédents(s) de 6 par \(f\) .
Indice
Lecture graphique d'images et d’antécédents.
Solution
\(f(4)=2,5\) donc l'image de 4 est 2,5.
Les antécédents de 6 sont les valeurs de \(x\) pour lesquelles \(f(x)=6\) : ce sont -3 et 5.
Question
La loi de Boyle-Mariotte indique qu'à température constante, si le gaz contenu dans un récipient passe d'un état (P1 , V1) à un état (P2 , V2) où P est la pression en pascals (Pa) et V le volume en mètres cubes (m3), alors P1 × V1 = P2 × V2 .
Le gaz contenu dans un ballon occupe un volume de 5 L lorsqu'on le place à l'air libre (donc à une pression P = 1 013 hPa). Un plongeur emporte ce ballon au fond de l'eau à une profondeur telle que la pression P est de 2 000 hPa.
Donner un ordre de grandeur du volume en litres occupé par le gaz contenu dans le ballon.
Indice
Appliquer la formule (produit en croix)
Indice
\(P_1\times V_1=P_2\times V_2\) équivaut à \(\displaystyle V_2=\frac{P_1\times V_1}{P_2}\)
Solution
environ 2,5 L
Solution
\(5\times 1013 = x\times 2000\) équivaut à \(\displaystyle x=\frac{5\times 1013}{2000}\approx\frac{5\times 1000}{2000} \)soit 2,5L
Question
Question
Déterminer l'équation réduite de la droite (EF) où E(4 ; 6) et F(–1 ; 3).
Solution
\(\displaystyle y=\frac{3}{5}x+\frac{18}{5}\)
ou
\(y=0,6x+3,6\)
Solution
Graphiquement
Le coefficient directeur vaut \(\displaystyle a=\frac{3}{5}=0,6\)
L'ordonnée à l'origine est à \(0,6\) au dessus de 3 donc \(b=3,6\)
Algébriquement
\(\displaystyle a=\frac{y_E-y_F}{x_E-x_F}=\frac{6-3}{4-(-1)}=\frac{3}{5}=0,6\)
donc \(y=0,6x+b\) et la droite passe par le point F(-1 ;3)
donc \(3=0,6\times(-1)+b\)
d'où \(3=-0,6+b\)
d'où \(3+0,6=b\)
on a donc \(b=3.6\) et donc \(y=0,6x+3,6\)