Exercice : MD4 - page 57
![]()
Question
Étudier le signe de \(-4n + 3\) suivant les valeurs de \(n\) .
Indice
résoudre \(-4n+3\leqslant 0\).
Solution
on a \(-4n+3\leqslant 0\) pour \(\displaystyle n \geqslant \frac{3}{4}\)
et \(-4n+3\geqslant 0\) pour \(\displaystyle n \leqslant \frac{3}{4}\)
Solution
\(-4n+3\leqslant 0\)
\(3\leqslant 4n\)
\(\displaystyle \frac{3}{4}\leqslant n\)
donc pour \(\displaystyle n \geqslant \frac{3}{4}\) on a \(-4n+3\leqslant 0\)
et pour \(\displaystyle n \leqslant \frac{3}{4}\) on a \(-4n+3\geqslant 0\)
Question
Question
Question
Le point A(3 ; 6) appartient-il à la courbe \(\mathcal{C}: y=\sqrt{7x+15}\) ? Justifier.
Solution
A appartient à \(\mathcal{C}\).
Solution
\(y=\sqrt{7x+15}\) est-elle vérifiée pour \(x=3\) et \(y=6\) ?
\(\sqrt{7\times 3+15}=\sqrt{36}=6\) donc l'équation de la courbe \(\mathcal{C}\) est vérifiée par les coordonnées de A : A appartient à \(\mathcal{C}\).
Question
Question
Calculer le taux équivalent à une diminution de 20 % suivie d'une autre augmentation de 10 %.
Indice
ou 10% correspond à un dixième
Solution
diminution de 12%
Solution
diminution de 20% : coefficient multiplicateur de 0,8
augmentation de 10% : coefficient multiplicateur de 1,1
\(0,8\times 1,1=0,88\) soit une diminution de 12%
ou
en partant de 100 : une diminution de 20% est une diminution de 20 ce qui donne 80.
en partant de 80, une augmentation de de 10% est une augmentation de 8.
Une diminution de 20 puis une augmentation de 8 donne au final une diminution de 12.
Question
Le diagramme suivant indique l'opérateur téléphonique choisi d'après un sondage sur 2 500 personnes :
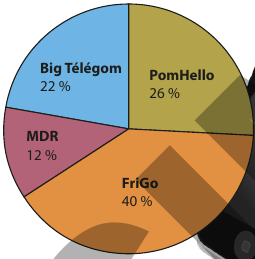
Indiquer le nombre de personnes qui ont souscrit un abonnement chez FriGo.
Indice
40% de 2 500
Solution
1000 personnes
Solution
40% de 2 500 donc \(\displaystyle \frac{40}{100}\times 2500=4\times250\) ce qui fait 1000.
Question
Résoudre \(4x^2 = 100\).
Indice
Deux méthodes :
Annuler le deuxième membre de l'égalité, factoriser l'identité remarquable et résoudre (produit nul)
Isoler \(x^2\) puis prendre la racine carrée et son opposé
Solution
S={-5 ; 5}
Solution
1ère méthode
\(4x^2=100\)
\(x^2=25\)
\(x^2-25=0\)
on remarque que \(x^2-25\) est l'identité remarquable \(a^2-b^2=(a-b)(a+b)\)
\((x-5)(x+5)=0\)
Un produit de facteur est nul si et seulement si un des facteurs est nul donc \(x=5\) ou \(x=-5\)
2ème méthode
\(4x^2 = 100\)
\(x^2=25\)
donc les deux solutions sont \(\sqrt{25}\) et \(-\sqrt{25}\)
Question
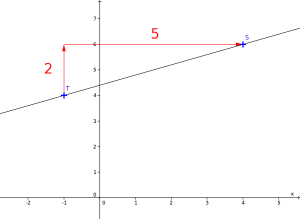
Déterminer l'équation réduite de la droite (ST) où S(4 ; 6) et T(‒1 ; 4).
Indice
en plaçant les points dans un repère et en lisant graphiquement l'équation de la droite
ou en mixant les deux méthodes
Solution
\(\displaystyle y=\frac{2}{5}x+\frac{22}{5}\)
ou
\(y=0,4x+4,4\)
Solution
Algébriquement
Algébriquement : \(y=ax+b\)
\(\displaystyle a=\frac{6-4}{4-(-1)}=\frac{2}{5}\)
donc \(\displaystyle y=\frac{2}{5}x+b\)
On choisit un des deux points : S(4 ; 6) par exemple. Il appartient à la droite donc ses coordonnées vérifient l'équation de la droite.
on a \(\displaystyle 6=\frac{2}{5}\times 4+b\) qui est une équation d’inconnue \(b\).
\(\displaystyle b=6-\frac{8}{5}\) donc \(\displaystyle b=\frac{6\times5}{5}-\frac{8}{5}=\frac{22}{5}\)
Question
Déterminer un ordre de grandeur de la vitesse d'un objet dont l'énergie cinétique est égale à 412 Joules (J) et de masse 51 kg.
Énergie cinétique (en J) : \(\displaystyle E_c=\frac{1}{2}mv^2\)
avec \(m\) : masse (kg) et \(v\) : vitesse (m/s).
Indice
Remplacer et résoudre l'équation
Solution
\(v\) vaut approximativement 4 m/s.
Solution
\(\displaystyle 412=\frac{1}{2}\times 51\times v^2\)
donc \(v^2=412 \times 2 \div 51\) ça donne approximativement \(400\times2\div50\) donc 16 et en prenant la racine carré (une vitesse est positive) : 4