MC2 - page 105 [Automatismes]

Exercice : MC2 - page 105

Question

Le prix d'un manteau passe de 50 € à 75 €. Calculer le pourcentage d'augmentation.

Indice

Comparer le montant de l'évolution au prix initial.

Solution

\(75-50=25\) et 25 est la moitié de 50 donc 50%

Question

Résoudre l'inéquation : \(1 − 3 x \leqslant 2 x − 3\).

Indice

Attention : si on divise les deux membres d'une inéquation par un nombre négatif, l'inéquation change de sens.

Astuce : regrouper les 'x' de façon à ce qu'ils aient un coefficient positif.

Solution

\(\displaystyle x\geqslant \frac{4}{5}\)

Solution

\(1 − 3 x \leqslant 2 x − 3\)

\(1 +3 \leqslant 2 x +3x\)

\(4\leqslant 5x\)

\(\displaystyle\frac{4}{5}\leqslant x\)

Question

Calculer 30 % de 60.

Indice

10% c'est un dixième (diviser par 10) donc 30% c'est .... dixièmes.

: Appliquer un pourcentage

Solution

Un dixième de 60 c'est 6 donc 30% c'est 3 dixièmes et \(3\times 6=18\)

Question

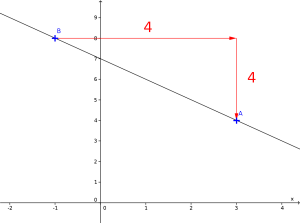
Déterminer l'équation réduite de la droite (EF) avec E(3 ; 4) et F(‒1 ; 8).

Solution

Méthode graphique

\(\displaystyle a=\frac{4}{4}=1\)

\(b=7\)

Méthode algébrique :

\(y=ax+b\) avec \(\displaystyle a=\frac{4-8}{3-(-1)}=\frac{-4}{4}=-1\)

\(\displaystyle y=-1x+b\) et (3 ; 4) appartient à la droite

\(\displaystyle 4=-1\times3+b\) donc \(\displaystyle b=4+3\)

\(\displaystyle y=-1x+7\)

Question

On considère la fonction \(f\) définie par \(f ( x ) = x ^2 + x\) . Déterminer \(\displaystyle\frac{f(2)-f(1)}{2-1}\)

Indice

Calculer \(f(1)\), \(f(2)\) et simplifier la fraction.

Solution

\(f ( 1 ) = 1^2 + 1=2\) et \(f ( 2 ) = 2 ^2 +2=6\)

donc \(\displaystyle\frac{6-2}{2-1}=\frac{4}{1}=4\)

Question

On augmente le prix d'un produit de 10 %, puis on réduit ce nouveau prix de 10 %. Indiquer s'il y a eu une évolution du prix initial et, si c'est le cas, préciser dans quel sens et de quel pourcentage.

Indice

Les 10% s'appliquent-ils à la même valeur ?

Évolutions successives de pourcentages

Solution

Indiquer s'il y a eu une évolution du prix initial

Il y a eu une évolution du prix.

justification : les 10% ne s'appliquent pas à la même valeur donc ne se compensent pas

Solution

préciser dans quel sens

C'est une réduction.

justification : la valeur à laquelle on applique l'augmentation est inférieure à celle à laquelle on applique la réduction donc la réduction est plus importante

Solution

et de quel pourcentage

de 1%

calcul : le coefficient multiplicateur correspondant à une augmentation de 10% est 1,1 et celui correspondant à une diminution de 10% est 0,9.

On multiplie les deux coefficients \(1,1\times 0,9=0,99\) donc une diminution de 1%.

(on sait que \(11\times 9=99\))

Question

Développer l'expression \(( x − 1)(2 − x ) + 2 x ( x +2)\).

Indice

Développer

Solution

\(x^2+7x-2\)

Solution

\(( x − 1)(2 − x ) + 2 x ( x +2)\)

\(2x-x^2-2+x\ +\ 2x^2+4x\)

\(x^2+7x-2\)

Question

On représente les deux droites D\(_1\) et D\(_2\) .

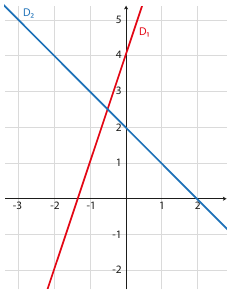
• Donner graphiquement les équations réduites des droites.

Indice

Lecture d'une équation de droite

Solution

D\(_1 :y=3x+4\)

D\(_2 :y=-x+2\)

Question

On représente les deux droites D\(_1\) et D\(_2\) .

• Déterminer par le calcul les coordonnées du point d'intersection des droites D\(_1\) et D\(_2\) .

Indice

Les coordonnées du point d'intersection des deux droites sont les solutions du système formé par les deux équations de droite.

Solution

\(\displaystyle\left( -\frac{1}{2} ; \frac{5}{2}\right)\)

Solution

On résout le système \(\left \{ \begin {array}{rcrcl} y & = & 3x&+&4 \\ y & = & -x&+&2 \end {array} \right.\)

équivaut à \(\left \{ \begin {array}{ccl} 3x+4& = & -x+2 \\ y & = & 3x+4 \end {array} \right.\)

équivaut à \(\left \{ \begin {array}{ccl} 3x+x& = & 2-4 \\ y & = & 3x+4 \end {array} \right.\)

équivaut à \(\left \{ \begin {array}{ccl} 4x& = & -2 \\ y & = & 3x+4 \end {array} \right.\)

équivaut à \(\left \{ \begin {array}{ccl} x& = &\displaystyle -\frac{1}{2} \\ y & = & \displaystyle 3\times \left(-\frac{1}{2}\right)+4 \end {array} \right.\)

équivaut à \(\left \{ \begin {array}{ccl} x& = &\displaystyle -\frac{1}{2} \\ y & = & \displaystyle\frac{5}{2} \end {array} \right.\)

Question

On représente les deux droites D\(_1\) et D\(_2\) .

• Le point A(8 ; 30) appartient-il à l'une des droites D\(_1\) et D\(_2\) ? Justifier.