Exercice : MC4 - page 125
Question
Soit \(f\) la fonction représentée ci-contre.
1_Déterminer graphiquement l'image de 0 par \(f\).
2_Déterminer graphiquement l'équation réduite de la droite.
3_Déterminer l'antécédent de 5 par \(f\).
4_Donner le signe de \(f\) sur [−2 ; 3].
Solution
1_
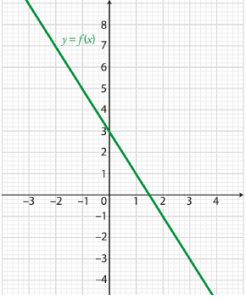
L'image de 0 est \(f(0)=3\).
2_
\(y=-2x+3\)
3_
L'antécédent de 5 est -1 : \(f(-1)=5\)
4_
La droite coupe l'axe des abscisses en \(x=1,5\) donc \(f(x)\geqslant 0\) sur [-2 ;1,5] et \(f(x)\leqslant 0\) sur [1,5 ;3].
\(\begin{array}{|l|l c c c r|}\hline x&-2&&1,5&&3\\\hline \text{signe de } f&&+&0&-&&\\\hline \end{array}\)
Question
Résoudre \(2 x^2 + 10 = 28\).
Indice
Deux méthodes :
Annuler le deuxième membre de l'égalité, factoriser l'identité remarquable et résoudre (produit nul)
Isoler \(x^2\) puis prendre la racine carrée et son opposé
Solution
S = { -3 ; 3 }
Solution
1ère méthode
\(2x^2+10=28\)
\(2x^2-18=0\)
\(2(x^2-9)=0\)
on remarque que \(x^2-9\) est l'identité remarquable \(a^2-b^2=(a-b)(a+b)\)
\(2(x-3)(x+3)=0\)
Un produit de facteur est nul si et seulement si un des facteurs est nul donc \(x=3\) ou \(x=-3\)
2ème méthode
\(2 x^2 + 10 = 28\)
\(2x^2=18\)
\(x^2=9\)
\(x=-\sqrt{9}\) ou \(x=\sqrt{9}\)
Question
Question
Question
Mettre au même dénominateur : \(\displaystyle\frac{2}{x − 1} −\frac{x}{ 3 − 2 x}\) .
Solution
\(\displaystyle\frac{-x^2-3x+6}{(x-1)(3-2x)}\)
Solution
\(\displaystyle\frac{2}{x − 1} −\frac{x}{ 3 − 2 x}\)
\(\displaystyle\frac{2 \times (3-2x)}{(x-1)(3-2x)}-\frac{x \times (x-1)}{(3-2x)(x-1)}\)
\(\displaystyle\frac{6-4x-(x^2-x)}{(x-1)(3-2x)}\)
\(\displaystyle\frac{-x^2-3x+6}{(x-1)(3-2x)}\)