MD2 - page 39 [Automatismes]

Exercice : MD2 - page 39

Question

On donne l'expression \(p_n = 2n–3\). Calculer \(p_7\) .

Question

Résoudre l'équation \(2x−1=4−5 x\)

Solution

\(2x-1=4-5x\)

\(2x+5x=4+1\)

\(7x=5\)

\(\displaystyle x=\frac{5}{7}\)

Question

Comparer les fractions \(\displaystyle \frac{3}{4}\) et \(\displaystyle \frac{5}{7}\)

Solution

\(\displaystyle \frac{5}{7} < \frac{3}{4}\)

On réduit au même dénominateur : \(\displaystyle \frac{3}{4}=\frac{3\times7}{4\times 7}=\frac{21}{28}\) et \(\displaystyle \frac{5}{7}=\frac{5\times 4}{7\times 4}=\frac{20}{28}\) puis on compare les numérateurs.

Question

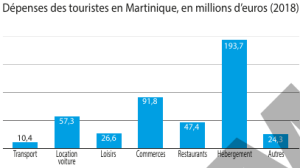
Il y a eu, en 2018, 1 046 735 touristes en Martinique. Les dépenses de ces touristes sont résumées par ce graphique.

Déterminer le pourcentage que représente l'hébergement dans ces dépenses.

Indice

l'hébergement par rapport au total

Solution

l’hébergement représente 42,9 % des dépenses.

Solution

On considère l'hébergement par rapport au total des dépenses en millions : \(\displaystyle \frac{193,7}{10,4+57,3+26,6+91,8+47,4+193,7+24,3}\) donc \(\displaystyle\frac{193,7}{451,5}=0,429\) et on exprime le résultat en pourcentage.

Question

Il y a eu, en 2018, 1 046 735 touristes en Martinique. Les dépenses de ces touristes sont résumées par ce graphique.

Calculer le montant moyen dépensé par chaque touriste.

Solution

431 €

Solution

On divise le total des dépenses exprimé en euros par le nombre de touristes : \(451,5\times10^6 \div 1\ 046\ 735=431\)

Question

Une facture de chauffage est passée de 1 500 € à 1 590 €. Donner le pourcentage d'augmentation.

Indice

transformer l'augmentation par rapport au prix initial en pourcentage (par rapport à 100)

Indice

Complément

On peut se reporter au cours de 2^nde concernant les évolutions en pourcentage.

Solution

Augmentation de 6 %.

Solution

Sans calculatrice

Le prix a augmenté de 90 € pour 1500 € donc pour obtenir l'augmentation en pourcentage il faut connaître l'augmentation pour 100 € donc pour 15 fois moins.

\(90\div 15 = 6\) donc 6 % d'augmentation.

Avec calculatrice (hors exercice)

On calcule le rapport entre le prix final et le prix initial : \(\displaystyle \frac{1590}{1500}=1,06\) et le coefficient multiplicateur 1,06 traduit une augmentation de 6 %.

Question

Un prix augmente successivement de 4 % puis de 25 %. Calculer le taux global d'augmentation.

Indice

On peut se reporter au cours de 2^nde concernant les évolutions en pourcentage.

Solution

30 %

Solution

On multiplie les coefficients traduisant les augmentations : \(1,04\times1,25=1,3\) soit une augmentation de 30 %.

Question

Déterminer l'équation réduite des droites \(D_1\) et \(D_2\).

Déterminer les coordonnées de leur point d'intersection.

Indice

Savoir lire une équation de droite

Utiliser les coefficients directeurs des deux droites pour calculer l'ordonnée du point d'intersection.

ou résoudre le système formé des équations des deux droites.

Solution

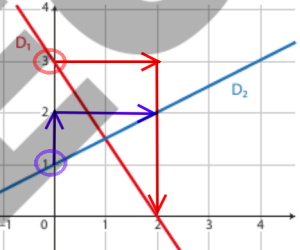
\(\displaystyle D_1 : y=-\frac{3}{2}x+3\)

\(\displaystyle D_2 : y=\frac{1}{2}x+1\)

Le point d'intersection a pour coordonnées \(\displaystyle \left( 1 ; \frac{3}{2} \right)\) ou (1 ; 1,5)

Solution

\(\displaystyle \textcolor{red}{D_1} : y=-\frac{3}{2}x+3\)

\(\displaystyle \textcolor{blue}{D_2} : y=\frac{1}{2}x+1\)

le coefficient directeur de \(D_1\) est -1,5 donc en partant de 3 à l'ordonnée à l'origine, l'ordonnée du point d'abscisse 1 est \(3-1,5=1,5\).

De même, le coefficient directeur de \(D_2\) est 0,5 donc en partant de 1 à l'ordonnée à l'origine, l'ordonnée du point d'abscisse 1 est \(1+0,5=1,5\).

Le point d'intersection est donc (1 ; 1,5) ou \(\displaystyle \left( 1 ; \frac{3}{2} \right)\)

Système

On résout le système \(\left \{ \begin {array}{rcrcl} y & = & -\frac{3}{2}x&+&3 \\ y & = & \frac{1}{2}x&+&1 \end {array} \right.\)

équivaut à \(\left \{ \begin {array}{ccc} \frac{1}{2}x+1 & = & -\frac{3}{2}x+3 \\ y & = & \frac{1}{2}x+1 \end {array} \right.\)

équivaut à \(\left \{ \begin {array}{ccc} (\frac{1}{2}+\frac{3}{2})x& = &3-1 \\ y & = & \frac{1}{2}x+1 \end {array} \right.\)

équivaut à \(\left \{ \begin {array}{ccc} 2x& = &2 \\ y & = & \frac{1}{2}x+1 \end {array} \right.\)

équivaut à \(\left \{ \begin {array}{ccc} x& = &1 \\ y & = & \frac{1}{2}\times 1+1 \end {array} \right.\)

équivaut à \(\left \{ \begin {array}{ccc} x&=&1 \\ y & = & \frac{3}{2} \end {array} \right.\)